Понимание фактора, связывающего две пропорциональные переменные
Фиксированная величина, устанавливающая прямую связь между двумя переменными, является фундаментальной в математике и различных научных дисциплинах. Эта величина, часто представляемая одной буквой, как «k», определяет, как одна переменная изменяется в прямом ответе на изменения в другой. Например, если пройденное расстояние (d) прямо пропорционально времени, затраченному (t), то соотношение выражается как d = kt. Значение «k» является константой пропорциональности. Оно диктует конкретную скорость изменения например, если k = 60, то для каждого пройденного часа (t) пройденное расстояние (d) составляет 60 миль.
Эта константа имеет решающее значение для прогнозирования и понимания отношений между величинами. В физике она позволяет вычислять скорость, ускорение и другие физические явления. В экономике она помогает моделировать отношения между переменными, такими как предложение и спрос. Её значение заключается в способности количественно определять точную природу пропорциональности между двумя переменными, допуская точные предсказания. Без этой константы отношения остаются описанными только в общих чертах. Следовательно, способность устанавливать и использовать эту константу повышает предсказуемость и удобство использования моделей.
Эта концепция лежит в основе большей части современного количественного анализа, позволяя перейти от простого наблюдения к проницательным предсказаниям и объяснениям.
Что такое постоянная пропорциональности
Понимание постоянной пропорциональности необходимо для распознавания и количественной оценки отношений между переменными.Это фиксированное значение диктует конкретную скорость изменения между двумя прямо пропорциональными величинами.
- Фиксированная стоимость
- Прямые отношения
- Темпы изменений
- Предсказательная сила
- Математическая модель
- Количественные изменения
- Постоянная пропорциональность
- Переменные отношения
Фиксированная величина, или постоянная, имеет основополагающее значение для выражения прямой связи между переменными. Эта скорость изменения, описывает ли она расстояние по отношению ко времени или цену по отношению к количеству, имеет важное значение для прогнозирования. Постоянная обеспечивает математическую модель для понимания того, как одна переменная реагирует на изменения в другой. Например, если расстояние (d) прямо пропорционально времени (t) с константой 60, уравнение d = 60t описывает отношения, допускающие вычисления. Количественное изменение имеет решающее значение в различных областях, от физики до экономики. Постоянная уточняет пропорциональность, обеспечивая точное предсказание. Эта константа, краеугольный камень математического моделирования, является неотъемлемой частью понимания и применения этих отношений в различных дисциплинах.
1. Фиксированная стоимость
Фиксированная величина в контексте пропорциональности представляет собой постоянную скорость изменения между двумя переменными. Эта постоянство является фундаментальным для понятия пропорциональности. Фиксированная величина, часто символизируемая как одна переменная (например, «k»), инкапсулирует врожденную связь между переменными. Это означает, что для каждого изменения единицы в одной переменной существует соответствующее, предсказуемое изменение в другой. Без этой фиксированной величины прямая пропорциональная связь не может быть точно определена или количественно. Разнообразная величина будет указывать на непропорциональную связь, где изменение в одной переменной не последовательно коррелирует с другой.
Рассмотрим сценарий, при котором стоимость яблок (С) прямо пропорциональна количеству яблок (n). Если одно яблоко стоит $1, то стоимость прямо пропорциональна количеству, а константа пропорциональности (k) составляет $1. Это означает, что уравнение C = 1n точно представляет соотношение, где стоимость всегда увеличивается на $1 за каждое дополнительное купленное яблоко. Это фиксированное значение $1 имеет решающее значение при расчете стоимости любого количества яблок, от одного до десятков. Такие фиксированные отношения жизненно важны во многих областях, от расчета площади прямоугольника (где константа — ширина или высота) до понимания скорости транспортного средства (где константа — скорость).
По сути, фиксированное значение выступает в качестве мультипликатора, определяющего удельное соотношение между переменными. Его наличие позволяет генерировать предсказуемые результаты на основе изменений в одной переменной. Понимание этого фиксированного значения жизненно важно для точного расчета, прогнозирования и моделирования в различных дисциплинах. Фиксированный характер этой константы пропорциональности обеспечивает определенность в отношении и предсказуемость результатов.
2.Прямые отношения
Прямая связь между двумя переменными означает, что по мере увеличения одной переменной другая увеличивается пропорционально, а, наоборот, по мере уменьшения одной, другая уменьшается пропорционально. Это последовательное, предсказуемое изменение является центральным для понятия константы пропорциональности. Понимание этой взаимосвязи имеет решающее значение для моделирования и прогнозирования различных явлений в науке, технике и экономике.
- Последовательное изменение темпов
Определяющей характеристикой прямой связи является последовательная скорость изменения. Это означает, что для каждой единицы увеличения или уменьшения одной переменной другая переменная изменяется на соответствующую, фиксированную величину. Эта последовательная скорость образует основу для определения постоянной пропорциональности. Например, если автомобиль движется с постоянной скоростью, пройденное расстояние прямо пропорционально времени, затраченному на путешествие; последовательная скорость изменения времени приводит к последовательной скорости изменения расстояния.
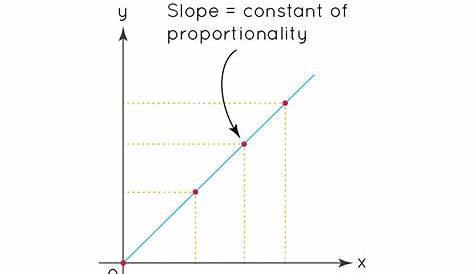
* Графическое представление
Графически прямая связь изображается прямой линией, проходящей через начало. Наклон этой линии непосредственно представляет постоянную пропорциональности. Более крутая линия указывает на большую константу, означающую более высокую скорость изменения. Это визуальное представление уточняет пропорциональную природу взаимосвязи и обеспечивает способ быстрой оценки силы связи между переменными.
* Математическая формула
Математически прямое отношение выражается как уравнение формы. y = хсгде k Это уравнение подчеркивает прямую связь между двумя переменными, y и x, облегчаемый постоянным kЭто уравнение является фундаментальным для расчета значения одной переменной, заданной другой и постоянной, или наоборот.
* Реальные приложения
Прямые отношения вездесущи в повседневных сценариях. Расход топлива транспортного средства (расстояние, пройденное за галлон), площадь квадрата (длина стороны квадрата) или стоимость предметов в продуктовом магазине на основе их количества (цена за товар) — все это иллюстрирует прямые отношения, где понимание постоянной пропорциональности имеет важное значение для точных расчетов и прогнозов.
В целом, константа пропорциональности неразрывно связана с понятием прямой связи. Константа количественно определяет конкретную скорость изменения между переменными, делая связь предсказуемой и позволяя математическое моделирование. Это понимание облегчает точные вычисления и предсказания в широком диапазоне контекстов.
3.Степень изменения
Постоянная пропорциональности инкапсулирует скорость, с которой одна переменная изменяется в ответ на изменение другой. Эта скорость изменения является фундаментальным компонентом, определяющим специфическую связь между переменными. Более высокая скорость изменения приводит к большей постоянной, подразумевая более существенное смещение одной переменной для каждой единицы изменения в другой. Например, в сценарии, где расстояние прямо пропорционально времени, высокая постоянная означает быстрое движение. И наоборот, меньшая постоянная отражает более медленное движение.
Рассмотрим транспортное средство, движущееся с постоянной скоростью. Расстояние, охватываемое (выход), прямо пропорционально прошедшему времени (вход). Скорость изменения расстояния на единицу скорости времени является постоянной пропорциональности. Транспортное средство, движущееся со скоростью 60 миль в час, имеет большую константу, чем одно, движущееся со скоростью 30 миль в час. Эта разница в скорости изменения непосредственно влияет на величину расстояния, охватываемого в заданном временном интервале. Аналогично, в бизнес-контексте скорость, с которой доход увеличивается относительно производства продукции, является постоянной пропорциональности; более высокая постоянная указывает на более эффективный производственный процесс или более высокую стоимость на единицу. Скорость изменения быстро изменяется в тандеме с другой, косвенно диктует величину постоянной пропорциональности. Поэтому понимание скорости изменения имеет решающее значение для понимания значения постоянной пропорциональности.
По сути, скорость изменения является ощутимым проявлением постоянной пропорциональности. Она диктует степень, в которой одна переменная изменяется относительно другой, что лежит в основе многочисленных практических применений. Признание этого взаимодействия между скоростью изменения и постоянной приводит к более глубокому пониманию взаимосвязи между переменными. Точное прогнозирование и эффективное моделирование опираются на это понимание; знание скорости изменения проясняет присущую пропорциональность и расширяет возможности количественного анализа в различных дисциплинах.
4.Прогнозирующая сила
Постоянная пропорциональности обеспечивает важнейшую основу для прогностической силы в различных областях. Она устанавливает точную взаимосвязь между переменными, позволяя точно оценивать будущие результаты на основе наблюдаемых тенденций. Понимание этой фиксированной взаимосвязи расширяет возможности прогнозирования, позволяя принимать обоснованные решения в различных областях.
- Количественные отношения
Константа пропорциональности количественно определяет точную зависимость между переменными. Эта количественная оценка необходима для предиктивного моделирования. Например, если скорость транспортного средства постоянна, пройденное расстояние прямо пропорционально пройденному времени. Константа пропорциональности в этом случае — сама скорость. Это позволяет точно прогнозировать, как далеко транспортное средство будет двигаться в заданный временной промежуток.
* Экстраполяция тренда
Установленные отношения позволяют экстраполировать тенденции. Если бизнес наблюдает последовательную связь между расходами на рекламу и ростом продаж, постоянная пропорциональность облегчает прогнозирование будущих продаж на основе прогнозируемых рекламных бюджетов. Исторические данные в сочетании с постоянной дают возможность оценивать за пределами наблюдаемого диапазона.
* Моделирование сценариев
Постоянная облегчает моделирование гипотетических сценариев. Понимание того, как переменные связаны через константу, позволяет прогнозировать при различных условиях. Например, в инженерии инженеры могут прогнозировать напряжение на структуру на основе ее свойств материала и ожидаемой нагрузки, используя константу пропорциональности, которая описывает реакцию материала на стресс. Это позволяет адаптировать и защитить конструкцию.
* Распределение ресурсов
Знание постоянной пропорциональности позволяет осуществлять обоснованное распределение ресурсов. Понимание взаимосвязи между ресурсами и результатами (например, использование удобрений и урожайность культур) позволяет оптимизировать распределение ресурсов, максимизировать эффективность и минимизировать отходы. В обрабатывающей промышленности это относится к использованию сырья для производства продукции, что позволяет лучше контролировать и улучшать планирование производства.
В целом, константа пропорциональности является краеугольным камнем прогностической силы. Ее способность количественно оценивать отношения, позволять экстраполировать тенденции, облегчать моделирование сценариев и направлять распределение ресурсов значительно повышает прогностические возможности в многочисленных приложениях. Понимая эту фиксированную взаимосвязь, организации и отдельные лица могут делать более точные прогнозы, улучшать принятие решений и оптимизировать результаты в различных контекстах.
5. Математическая модель
Математическая модель — это представление реального явления с использованием математических понятий и языка. Она упрощает сложность идентификации ключевых отношений, позволяя прогнозировать и понимать. Константа пропорциональности является важнейшим компонентом во многих математических моделях, воплощая фиксированное соотношение между переменными. Точная количественная оценка этой взаимосвязи является фундаментальной для точности модели и предиктивной мощности.
- Переменные и их взаимодействие
Математические модели явно определяют вовлечённые переменные и их взаимосвязи. Постоянная пропорциональности уточняет точный характер этого взаимодействия. Например, в модели движения автомобиля расстояние (d) и время (t) являются переменными, связанными скоростью (k), выраженной как d = kt. Постоянная «k» представляет собой фиксированное значение скорости автомобиля, определяющее, как изменяется расстояние со временем. Способность модели предсказывать будущее расстояние на основе времени напрямую зависит от знания этой постоянной.
* Предсказательные способности
Четко определенная модель, включающая константу пропорциональности, дает возможность прогнозировать. Модель может прогнозировать будущие значения одной переменной заданными значениями другой, исходя из установленной пропорциональности. Эта предсказательная способность очевидна в различных областях, от физики (прогнозирование траекторий снарядов) до экономики (прогнозирование спроса на основе цены). Точность прогноза зависит от точности и соответствующего выбора константы пропорциональности.
* Упрощение и идеализация
Математические модели упрощают реальные сценарии. Они часто идеализируют условия, предполагая, что определенные факторы остаются постоянными. Константа пропорциональности играет ключевую роль в этих упрощениях, поскольку она представляет идеализированное соотношение между переменными при конкретных обстоятельствах. Например, модель простого гармонического движения предполагает постоянную массу и пружинную жесткость. Константа пропорциональности инкапсулирует это идеализированное поведение.
* Модульная уточнение и валидация
Модели можно уточнять и валидировать, сравнивая их предсказания с реальными данными. Константа пропорциональности является центральной для этого процесса. Путем корректировки значения постоянной в модели можно улучшить ее предиктивную мощность. Если модель не в состоянии точно соответствовать наблюдаемым данным, точность постоянной должна быть поставлена под сомнение, что приводит к уточнению модели и более глубокому пониманию явления.
По сути, математическая модель, особенно касающаяся пропорциональности, опирается на константу пропорциональности, чтобы точно представлять соотношение между переменными.Это фиксированное значение жизненно важно для прогнозирования, упрощения и проверки модели на реальность. Успех модели зависит от правильной идентификации и использования постоянной, что позволяет более точно представлять и прогнозировать, в конечном итоге улучшая понимание и контроль над сложными системами.
6. Количественные изменения
Количественное изменение является фундаментальным для понимания константы пропорциональности. Это понятие означает, что изменения в одной переменной непосредственно связаны с соответствующими, измеримыми изменениями в другой. Константа пропорциональности воплощает в себе эту предсказуемую зависимость, позволяющую производить точные вычисления и прогнозы. Количественное изменение, следовательно, необходимо при определении константы пропорциональности и применении ее принципов к различным контекстам.
- Последовательное отношение
Количественное изменение отражает последовательную зависимость между переменными. Например, если стоимость яблок прямо пропорциональна количеству купленных яблок, каждое дополнительное яблоко добавит точно поддающуюся исчислению сумму к общей стоимости. Эта согласованность позволяет установить постоянную пропорциональности, позволяющую прогнозировать общие затраты на основе количества яблок.
* Измеримое воздействие
Изменения должны быть измеримы для значимого применения пропорциональности. Если расстояние увеличивается со временем, увеличение расстояния должно быть количественно измерено в единицах, таких как мили или километры, чтобы установить постоянную пропорциональности, представляющую скорость. Эта измеримость имеет решающее значение для прогнозирования и контроля.
* Предсказательное моделирование
Количественное изменение дает возможность прогнозного моделирования. Наблюдая, как одна переменная изменяется последовательно с другой, становится возможным создание математических моделей, которые точно предсказывают будущие значения. Например, знание постоянной пропорциональности расхода топлива и пройденного расстояния позволяет водителю предсказать количество топлива, необходимое для конкретной поездки.
* Контроль и оптимизация
Понимание количественных изменений обеспечивает механизмы контроля и оптимизации. Признание того, что изменения предсказуемы, позволяет корректировать одну переменную для управления другой. В производстве, например, знание того, сколько сырья необходимо для каждого блока продукта, позволяет менеджерам по производству оптимизировать использование ресурсов.
В заключение, количественное изменение имеет важное значение для определения и применения постоянной пропорциональности. Его наличие гарантирует, что отношения между переменными являются последовательными, измеримыми и предсказуемыми, что позволяет разрабатывать точные модели, давать возможность прогнозировать и облегчать контроль и оптимизацию во многих областях. Без количественного изменения концепция постоянной пропорциональности теряет свою практичность и предсказательную силу.
7.Постоянная пропорциональность
Термин «постоянная пропорциональности» непосредственно относится к фиксированному значению, которое устанавливает прямую связь между двумя переменными. Эта постоянная воплощает фундаментальное понятие пропорциональности, отношения, где изменение одной переменной последовательно соответствует предсказуемому изменению другой. Постоянная инкапсулирует скорость изменения; большая постоянная указывает на более быструю скорость изменения. Без этой постоянной отношение остается описательным утверждением, а не точной математической моделью. Например, если расстояние (d) прямо пропорционально времени (t), уравнение d = kt выражает это отношение, где «k» является постоянной пропорциональности. Эта постоянная, следовательно, является незаменимым компонентом в определении того, что составляет константу пропорциональности.
Значение постоянной пропорциональности очевидно в различных приложениях. В физике она количественно определяет такие отношения, как скорость (постоянство пропорциональности между расстоянием и временем). В экономике моделирует соотношение между спросом и предложением или стоимость товара на основе количества. В инженерии критически важно определить отношения между силой, ускорением и массой. Правильное понимание этой постоянной позволяет строить точные математические модели, отражающие реальность и позволяющие прогнозировать будущее поведение. Например, понимание постоянной пропорциональности между количеством используемых удобрений и урожайностью культур позволяет фермерам оптимизировать распределение ресурсов и максимизировать производство.
В заключение константа пропорциональности — это не просто математическая абстракция; это критический элемент в понимании и количественной оценке реальных отношений. Её точное определение позволяет строить надежные математические модели, расширяя возможности прогнозирования, оптимизации и принятия обоснованных решений в различных областях. Путем идентификации и применения константы пропорциональности достигается более глубокое понимание врожденных связей между переменными, что приводит к большей точности прогнозирования и практическому применению в различных контекстах.
8. переменные отношения
Переменная зависимость образует основу понятия пропорциональности. Она описывает, как изменения в одной переменной последовательно и предсказуемо влияют на другую. Эта взаимосвязь имеет основополагающее значение для определения постоянной пропорциональности. Переменная связь подразумевает прямую связь, где последовательное изменение одной переменной приводит к соответствующему изменению другой. Например, если пройденное расстояние (переменная) увеличивается со временем (другая переменная), эта взаимосвязь лежит в основе понятия скорости как константы пропорциональности.
Важность переменной зависимости как компонента постоянной пропорциональности проистекает из ее способности количественно определять конкретную скорость изменения. Эта норма является постоянной. Рассмотрим цену товара на единицу. Цена, скажем, апельсинов напрямую связана с количеством купленных. Скорость, при которой общая стоимость увеличивается с количеством купленных апельсинов (например, $1,50 за апельсин) устанавливает постоянную пропорциональности. Эта зависимость, выраженная математически, позволяет прогнозировать общую стоимость для любого количества апельсинов. Ключевое значение имеет то, что последовательный характер этой взаимосвязи как количества изменяется, изменения стоимости предсказуемо необходимы для определения постоянной. По сути, четкая переменная зависимость необходима для идентификации и расчета постоянной пропорциональности.
Практическая значимость понимания переменных отношений и их связи с константой пропорциональности пронизывает многочисленные поля. В физике фундаментально понимание движения, где скорость — постоянная пропорциональности расстояния и времени. В экономике помогает понять, как взаимодействуют спрос и предложение. В инженерии важно проектировать системы, где взаимосвязь между переменными должна быть предсказуемой и поддающейся количественной оценке, как стресс и деформация в материалах. Точное моделирование и прогнозирование в этих и других областях зависит от точной характеристики этой прямой связи и идентификации соответствующей постоянной.
Часто задаваемые вопросы о постоянной пропорциональности
В этом разделе рассматриваются общие вопросы относительно постоянной пропорциональности, предлагая краткие и информативные ответы.
Вопрос 1: Что такое постоянная пропорциональности и почему она важна?
Постоянная пропорциональности — это фиксированное значение, устанавливающее прямую связь между двумя переменными. Эта постоянная количественно определяет скорость изменения между переменными, позволяя делать точные прогнозы и вычисления.В различных областях, от физики до экономики, понимание этой постоянной имеет решающее значение для моделирования, прогнозирования и оптимизации результатов.
Вопрос 2: Как определяется постоянная пропорциональности?
Постоянная пропорциональности определяется путем идентификации последовательного соотношения между переменными. Для прямой связи константа вычисляется путем деления значения одной переменной на соответствующее значение другой. В математических терминах, если y = хсТогда k является константой, полученной k = y/x.
Вопрос 3: Что означает, когда отношения описываются как прямо пропорциональные?
Прямо пропорциональная связь означает, что по мере увеличения одной переменной пропорционально увеличивается другая. И наоборот, уменьшение одной переменной приводит к пропорциональному уменьшению другой. Эта последовательная связь является фундаментальной при определении постоянной пропорциональности, которая количественно определяет эту скорость изменения. График такой связи представляет собой прямую линию, проходящую через происхождение.
Вопрос 4: Существуют ли различные типы пропорциональности, и если да, то как они различаются?
В то время как прямая пропорциональность часто встречается, существуют и другие отношения. Обратная пропорциональность, например, описывает отношения, где при увеличении одной переменной пропорционально уменьшается другая. Основные различия возникают в математических формах и характерных графических представлениях, которые демонстрируют различные закономерности изменения. Понимание этих различий важно для выбора соответствующей модели для анализа конкретного сценария.
Вопрос 5: Каковы реальные приложения постоянной пропорциональности?
Многочисленные приложения реального мира используют константу пропорциональности. Расчет пройденного расстояния с учетом скорости и времени, определение стоимости предметов на основе количества и понимание взаимосвязи между давлением и объемом в газе являются наглядными примерами. Эта концепция является неотъемлемой частью различных дисциплин, включая физику, инженерию, экономику и многое другое.
Понимание постоянной пропорциональности обеспечивает основу для количественной оценки и прогнозирования отношений между переменными, позволяя ценную информацию в широком диапазоне приложений.
Далее мы рассмотрим конкретные приложения этой важной математической концепции.
Заключение
Постоянная пропорциональности служит краеугольным камнем для понимания и количественной оценки отношений между переменными. Это фиксированное значение инкапсулирует согласованную скорость изменения между двумя прямо пропорциональными величинами. Исследование этой концепции раскрывает ее решающую роль в математическом моделировании, позволяя точные прогнозы и оценки в различных дисциплинах. Ключевые идеи включают идентификацию согласованного соотношения между переменными, согласованный характер отношений, количественную оценку изменений и значение для прогностического моделирования. Постоянная пропорциональности является не просто математической абстракцией; она представляет собой фундаментальный принцип, который лежит в основе многочисленных приложений, от вычисления расстояний до прогнозирования потребностей в ресурсах, иллюстрируя ее всепроникающую важность в различных областях.
Дальнейшее исследование константы пропорциональности обещает еще большее понимание сложных отношений. Способность точно моделировать и прогнозировать на основе определенных констант будет продолжать стимулировать достижения в областях, начиная от научных исследований до инженерного проектирования. Продолжение исследования и применение этой фундаментальной концепции, несомненно, приведет к дальнейшим усовершенствованиям и открытиям в предстоящие годы.
ncG1vNJzZmivp6x%2Fb8DAnqqaZpOkum%2Bu0WiYp6aRYrG2s8aeqWitnpmys7%2FTmqWdoZ6cerW0xGaaqKajqa6vwIyonWaooqS9sL7ToqanmZyewbp6x62kpQ%3D%3D